Précision de vocabulaire
La forme de la Terre est une question de géodésie – la science qui étudie la forme et les dimensions de notre monde. Et, pour les géodésiens, cette forme est celle qu’il aurait dans l’espace si sa surface était en tout point à l’altitude 0 : elle ne présenterait aucune pente et serait donc, pour ainsi dire, horizontale. C’est de cette forme horizontale dont il est question ici.
La Préhistoire
Au commencement, tout poussait l'Homme à croire que la Terre était plate : l’horizon marin est plat et, sans les reliefs, on ne monterait ni ne descendrait jamais.
L’Antiquité classique (600 av. JC–100)
Il est difficile de déterminer avec certitude qui est le premier à supposer que la réalité pouvait être différente. Peut-être Thalès (vers 600 av. JC), mais il est sûr qu’Anaximandre, son successeur à l’école de Milet, imagine que nous vivons sur la section plane supérieure d’un cylindre qui flotte dans l’espace car "il n’a nulle part où tomber". Ensuite, Pythagore (vers 550 av. JC) conçoit un monde sphérique et Parménide (vers 500 av. JC) soutient l’hypothèse par des arguments rationnels. Mais comment a-t-il raisonnablement pu défendre une idée aussi contre-intuitive ?
Installé à Elée, en Italie, il constate d’abord que, lorsque l’on navigue de chez lui vers le Sud, les sommets des monts Nébrodes apparaissent sur l’horizon avant la plage de Sicile. Une seule explication, très simple, à ce phénomène : une courbure de la Terre dans le sens Nord–Sud.
Fort de cette observation, Parménide réalise une autre déduction bien moins évidente. Lorsque le Soleil se couche là où, plus tard, s’élèvera la ville de Naples, on le voit descendre dans le ciel et disparaitre sous l’horizon ; mais on constate en se retournant que le Mont Somma (actuellement le Vésuve) est en revanche encore éclairé et disparait dans l’ombre, depuis la base vers le sommet, en approximativement quatre minutes. Or, dans un schéma de Terre plate, la limite de l’ombre est nécessairement la projection du bord du monde et la trigonométrie offre la possibilité d’en calculer la distance ; à condition toutefois de connaître l’altitude du Mont Somma.
Fort heureusement, l’application du théorème de Thalès fait des miracles en la matière. Parménide découvre ainsi que le bord de la Terre devrait se situer à environ 75 km à l’Ouest. Dès lors, la Corse plonge dans le vide sidéral, tout comme la Gaule, la péninsule ibérique et l’océan qui se trouve au-delà – et dont, d’ailleurs, on ne distingue toujours pas la fin.
Bref, l’incohérence du résultat réfute l’hypothèse du calcul : la Terre n’est pas plate d’Est en Ouest et présente donc également une courbure dans ce sens. Or la figure géométrique la plus simple qui présente deux courbures perpendiculaires est la sphère. Nul doute pour Parménide que ce doit être la réalité. En outre, il en propose une modélisation climatique complète.
La théorie des cinq climats de Parménide
En prolongeant la courbe de la température moyenne en Europe jusqu’aux latitudes extrêmes, Parménide déduit un climat glacial aux pôles et une zone torride au niveau de l’Équateur. Ainsi, la Terre ne pourrait être habitable qu’aux latitudes moyennes des deux hémisphères. Au IIe siècle av. JC, Cratès de Mallos envisage l’existence d’un continent miroir du nôtre dans l’hémisphère sud. Mais la torride zone équatoriale étant considérée infranchissable, Cratès de Mallos conclut que sa supposition est promise à toujours rester hors de portée d’une vérification expérimentale.
Mais admettons-le : l’intuition de Parménide ne rencontre pas beaucoup d’adhésion. Toutefois, quelques décennies plus tard, l’un de ses élèves se range aux arguments de son maître et convainc l’ensemble du monde grec : Socrate (470–399 av. JC).
Les savants les plus réactifs ne tardent pas à poser la question subsidiaire évidente : la Terre étant sphérique, quelle est sa circonférence ?
Le premier à en donner une estimation est Eudoxe (408–355 av. JC), qui l’évalue à 400 000 stades – soit 74 000 kilomètres, presque le double de la réalité. Il est difficile de savoir comment il a obtenu ce résultat, car le détail de ses travaux a été perdu, mais il est probable qu’il ait mesuré la hauteur d’une étoile en différents endroits d’un même méridien.
Le phénomène de réfraction atmosphérique, encore inconnu à son époque, a pu fausser ses observations et le conduire à cette nette surestimation. Quoi qu’il en soit, étant la seule valeur disponible pendant quelques décennies, elle est reprise par les savants suivants et, notamment, par celui dont la Science va dépendre pendant plusieurs siècles : Aristote (384–322 av. JC).
L’illumination d’Ératosthène
Le premier calcul encore aujourd’hui documenté des dimensions de la Terre est l’œuvre d’Ératosthène (276–194 av. JC).
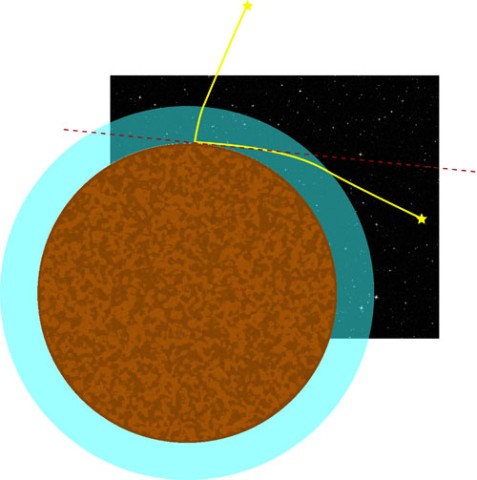
En visite à Syène (Assouan), Ératosthène est ébloui par le reflet du soleil au fond d’un puits. Effectivement : le jour du solstice d’été, le soleil de midi est au zénith d’Assouan, car la ville est située sur le Tropique du Cancer. Il remarque en outre que le Soleil n’est jamais à la verticale d’Alexandrie. Grâce à l’absence de parallaxe du soleil, on sait que ses rayons peuvent être considérés comme parallèles entre eux et qu’il doit donc se trouver très loin de la Terre. S’il n’est jamais à la verticale d’Alexandrie, ce ne peut donc être que l’effet de la courbure de la Terre.
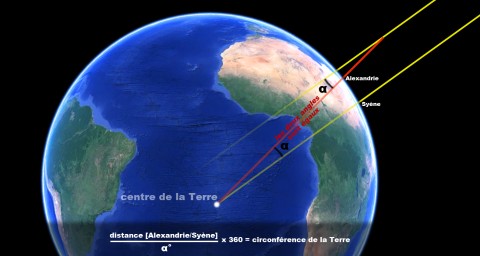
En mesurant la longueur de l'ombre d'un gnomon le jour du solstice d’été à Alexandrie, il déduit l’angle qui la sépare d’Assouan par la règle des angles alternes-internes. Il mesure ensuite la distance entre les deux villes pour ensuite la convertir sur 360° et obtenir la circonférence polaire de la Terre.
Ensuite, les récits divergent : parfois on dit qu’il a mesuré la distance en pas de chameau ou qu’il a utilisé ceux d’une armée. Mais il a également pu la calculer avec des plans cadastraux de l’époque, le Cadastre ayant justement été inventé sur les rives du Nil à cette époque.
Il détermine ainsi une circonférence terrestre de 252 000 stades, soit environ 42 000 kilomètres : une excellente précision pour les moyens de l’époque. Mais il ne s’agit là que d’un bienheureux hasard, car il a commis plusieurs approximations qui, par chance, se sont compensées entre elles. Mais ni lui ni personne ne pouvait être sûr de la fiabilité de son calcul, qui donne rapidement lieu à critiques et conduira à une nouvelle mesure du monde…
Peu de temps après Ératosthène, Hipparque (190–120 av. JC) fait sensiblement progresser les conditions scientifiques de notre connaissance de la forme de la Terre. Comme il est impossible de représenter une sphère sur un plan sans induire de déformations, Hipparque étudie les projections de base : coniques, cylindriques et azimutales. Il formalise une idée d’Ératosthène, qui avait représenté le monde en se servant de lignes remarquables Est–Ouest et Nord–Sud, et invente ainsi le système de coordonnées à base de parallèles et de méridiens qui est encore utilisé de nos jours. Par comparaisons des éclipses lunaires et solaires selon une méthode inventée par Aristarque de Samos (310–230 av. JC), il calcule la distance de la Terre à la Lune en commettant une erreur de moins de 10 %.
Et pendant ce temps, la mesure d’Ératosthène fait toujours débat. Posidonius (135–51 av. JC) reprend le calcul de la circonférence en mesurant la hauteur de la très brillante étoile Canopus à Rhodes et à Alexandrie. Il intègre la réfraction atmosphérique dans ses mesures, évalue à 5 000 stades la distance entre les deux villes et tient compte de leur décalage sur le méridien. Ses travaux confirment ceux d’Eratosthène, qui seront pérennisés par Strabon en 20 ap. JC.
Pendant ce temps… à Pékin
Trois théories de la forme de la Terre se succèdent durant l’antiquité chinoise. D’abord celle de la canopée (300 av. JC), qui présente ciel et terre sous forme d’arches. Puis ZHANG Heng (78–139) se représente le ciel comme un œuf dont la Terre serait le jaune. Enfin, la théorie Xuan Ye, d’origine obscure, propose un espace sans limite où flottent les corps célestes.
YI Xing (683–727) semble être le premier à réaliser une mesure de la circonférence terrestre en Chine, qu’il estime à environ 47 630 km.
En perfectionnant un appareil inventé dès le IIIe siècle, SHEN Kuo (1031-1095) met au point le compas à aiguille magnétique, qui deviendra la boussole. Il met en évidence la précession des équinoxes et découvre la formation des terrains par sédimentation marine.
L’Antiquité tardive (100–476)
Au IIe siècle, l’école d’Alexandrie rédige un grand ouvrage de Géographie, baptisé en référence au géant de la mythologie grecque : Atlas. Marin de Tyr (70–130), l’un de ses premiers rédacteurs, approuve les mesures rapportées par Strabon. Toutefois, bien qu'elles soient cohérentes entre elles, elles ne sont pas exprimées dans la même unité. Ainsi, les 240 000 stades d'Ératosthène correspondent à 180 000 chez Posidonius. Cette difficulté étant source de confusion, elle conduit Marin de Tyr à faire une erreur au terme de laquelle la circonférence du globe est réduite à 28 000 km.
Quelques années plus tard Claude Ptolémée (90–168) achève l’Atlas. Il sera pendant longtemps considéré comme le maître de la géographie, en dépit de ses imprécisions qui resteront méconnues pendant plusieurs siècles.
La double erreur de Ptolémée
Ptolémée étend sa cartographie jusqu’à l’Extrême-Orient. N’y étant pas allé en personne, il sous-estime les difficultés de la route empruntée par les voyageurs dont il recueille les témoignages, ce qui le conduit à évaluer la distance du Japon à environ 14 000 km, au lieu des 10 000 réels.
Or, en traçant un continent plus étendu qu’il n’est sur la sphère trop petite de Marin de Tyr, la distance par la mer entre les extrémités du continent diminue fortement.
Cette double erreur aura une conséquence très inattendue 1 400 ans plus tard…
Le Haut Moyen-Âge (476–987)
Avec le déclin de la civilisation grecque, la recherche fondamentale tombe en désuétude car la culture romaine est davantage tournée vers l’expérimentation pratique. Puis, la chute de l’empire d’Occident (476) met un terme à l’administration à grande échelle de Rome et les Européens se réorganisent autour d’économies locales. Les voyages cessent et, dès lors, la cartographie scientifique est abandonnée, faute d’utilité.
Si les recherches sur les dimensions de la Terre vont rester au point mort pendant plus de mille ans, le Moyen-Âge ne va pas pour autant oublier l’héritage grec. Contrairement à une idée reçue depuis trop longtemps, la connaissance de la sphéricité de la Terre ne s’est pas perdue au cours de cette période. Divers documents l'attestent :
- Au IVe siècle, Lactance tente d’imposer l’idée d’une Terre plate afin de faire table rase du passé paganiste. Il se moque de ceux qui pensent que la Terre est ronde, c’est-à-dire tous les gens instruits – lui excepté.
- De la même manière, dans sa Topographie Chrétienne, Cosmas Indicopleustès, un géographe improvisé du VIe siècle qui s’oppose avec virulence au christianisme officiel, déplore que nombre de savants font encore confiance aux idées antiques. Il propose également une carte d’un monde plat.
- Toutefois, l’archevêque Photius de Constantinople (IXe siècle) n’hésitera pas à qualifier les travaux de Cosmas d’"inepties" et d’"absurdités".
- Au XIIe siècle, les enluminures d’Hildegarde von Bingen montrent une Terre sphérique.
- Au XIIIe, le principal ouvrage d’astronomie du Moyen-Âge De Sphaera Mundi de Jean de Halifax est largement inspiré des écrits de Ptolémée.
- Enfin, l’Imago Mundi du cardinal Pierre d’Ailly (1410) cite Jean de Halifax et Ptolémée.
Si l’Atlas de Ptolémée disparait des bibliothèques occidentales pour ne faire son retour qu’à la fin du XIVe siècle, il reste en revanche trace des travaux d’Alexandrie et, plus encore, du Timée de Platon qui décrit et explique très bien la sphéricité du monde.
Le Moyen-Âge classique (987–1272)
Dès le XIe siècle, l’Occident met au point la pensée scolastique, dont la principale référence scientifique est Aristote. Dans son Traité du Ciel, il a affirmé la sphéricité de la Terre – ainsi que le géocentrisme, qui restera longtemps la seule représentation acceptée du système solaire.
Pendant ce temps… à Bagdad
Par son histoire et sa proximité à la Méditerranée, l’empire arabe bénéficie des découvertes grecques et acquiert ainsi la connaissance de la sphéricité de la Terre dès son origine.
Le calife Al-Mamûn (786–833) propose une vérification des travaux d’Ératosthène mais les premiers calculs réalisés restent approximatifs, accusant des erreurs d’entre -20 et +10%.
Al-Khwarizmi (780–850) donne la meilleure estimation arabe de l’époque, de 44 064 km.
Déjà très en avance sur son temps, l’astronomie arabe progresse avec Ibn Yunus (950–1009), qui estime avec une bonne précision diverses constantes fondamentales, dont l’angle de l’écliptique et la période de précession des équinoxes.
Le planisphère d’Al-Idrissi (1100–1165) succède à celui de Ptolémée et innove en développant la théorie des climats et en portant des informations de géographie humaine.
À la même époque, la féodalité se stabilise dans les royaumes francs. Les chevaliers répondent alors en masse à l’appel des croisades, qui sont à l’origine de la reprise de la cartographie scientifique en Occident. Car, s’il reste possible de naviguer jusqu’en Terre Sainte en longeant les côtes bien connues de la Méditerranée, les contacts directs avec l’empire arabe ont une conséquence inattendue : parmi les richesses que les croisés rapportent avec eux figurent des épices d’Extrême-Orient qui relèvent une cuisine occidentale plutôt fade. Elles connaissent un succès retentissant dans les cours d’Europe et deviennent un signe de richesse dont les monarques ne peuvent bientôt plus se passer.
Un commerce débute alors avec l’empire arabe. La rapidité et l’optimisation des voyages deviennent des atouts majeurs qui conduisent les Occidentaux à exhumer la cartographie scientifique. Les portulans, cartes marines d’un nouveau genre, sont alors établies : grâce à la boussole nouvellement arrivée de Chine par l’intermédiaire des vikings, les navires suivent des routes à cap constant et les temps de trajet de port à port se traduisent en distances. Les approximations de la méthode sont progressivement moyennées avec les répétitions des voyages. Au début du XIIIe siècle, les portulans présentent une excellente précision cartographique.
Le Bas Moyen-Âge (1272–1453)
Les cartes terrestres restent en revanche en leur état antique et ne s’enrichissent que de rares nouveautés. L’évolution la plus significative se produit au début du XIVe siècle, lorsque Marco Polo (1254–1324) revient de son voyage de prospection commerciale en Extrême-Orient.
Mais la question des dimensions de la Terre n’est pas encore reprise lorsque l’âge d’or médiéval, parfois appelé la Renaissance du XIIe, est stoppé par la Guerre de Cent Ans. À la fin du XIIIe siècle, seul le Sud de l’Europe continue à entretenir des échanges avec l’Orient.
La Renaissance (1453–1633)
Mais les intérêts des pays méridionaux restent divergents car, si le commerce par la Méditerranée fait les affaires des Vénitiens et des Génois qui s’imposent vite comme seuls intermédiaires européens, il est nettement moins avantageux pour les deux pays de la péninsule ibérique : en bord de carte, ils paient les épices au prix fort et, dès le XVe siècle, le roi Henri le Navigateur lance le Portugal à la recherche d’une route directe vers les richesses d’Extrême-Orient. Les explorateurs se succèdent toujours plus au Sud le long des côtes africaines.
En 1441, la découverte de la verdoyante Guinée par Nino Tristaõ balaie la théorie des cinq climats que Ptolémée avait relayée dans son atlas. En 1488, Bartolomeu Dias franchit le Cap de Bonne-Espérance.
Les expéditions portugaises barrent le passage aux initiatives de l’Espagne dont la situation économique menace dès lors de devenir critique, entraînant à brève échéance la fin de sa domination en Europe.
À la fin du XVe siècle, un Génois se met au service d’Isabelle de Castille pour tenter de devancer le Portugal en rejoignant l’Extrême-Orient par l’Ouest. Il a une absolue confiance en la mesure de Marin de Tyr, rapportée en dernier lieu par Pierre d’Ailly. Par ailleurs, selon l’étendue du continent eurasiatique de Ptolémée, il estime les Indes à une distance de 1 780 lieues marines, soit au plus deux mois de navigation.
La reine d’Espagne reste dubitative, car les découvertes portugaises ont jeté le doute sur l’ensemble des travaux d’Alexandrie. Il n’est pas simple pour un bateau de tenir la mer sans escale pendant deux mois ; et si le globe devait se révéler presque trois fois plus vaste, comme Aristote l’a écrit, l’expédition serait à coup sûr vouée à l’échec. Mais le comptable de la reine calcule ce que le succès du voyage ferait économiser à l’Espagne en termes de court-circuitage des intermédiaires. Elle ordonne alors la construction d’une caraque et de deux caravelles afin d’envoyer le Génois Christophe Colomb à la conquête de l’Ouest.
Lorsqu’il aborde une terre le 12 octobre 1492 après cinq semaines de navigation, c’est la promesse d’une rapide fortune pour l’Espagne. Mais ses descriptions ne correspondent en rien à l’Extrême-Orient de Marco Polo et provoquent la confusion parmi les géographes.
Il meurt en 1506 sans jamais avoir compris ce qu’il avait découvert et la lumière ne jaillit que l’année suivante : il existe entre l’Occident et l’Orient un continent dont nul ne soupçonnait l’existence – du moins officiellement.
Le destin inattendu d’Amerigo Vespucci
Le marchand Amerigo Vespucci embarque pour les terres découvertes à l’Ouest afin d’en prospecter les possibilités commerciales.
En 1503, le rapport qu’il envoie à son commanditaire Lorenzo de Médicis après son second voyage est titré Mundus Novus car "c’est là chose absolument nouvelle pour ceux qui en entendent parler". Cette inspiration aussi lumineuse que fortuite lui vaut d’être hissé quatre ans plus tard au rang de célébrité.
Son nom est ensuite abusivement utilisé au point que beaucoup finissent par croire que c’est lui qui a découvert ce nouveau continent.
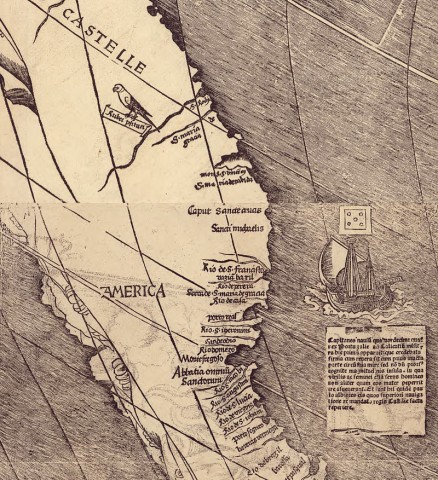
Dans l’école de géographie lorraine de Saint-Dié, le cartographe Martin Waldseemüller lui rend hommage en créant un néologisme pour nommer la baie de Rio de Janeiro : America. Ce nom circule, s’amplifie et, quelques années plus tard, s’impose comme celui de l’ensemble du continent.
Si la dernière décennie du XVe siècle avait failli approuver la mesure de la circonférence terrestre de Marin de Tyr, le siècle suivant ré-ouvre aussitôt la question. Toutefois, l’Amérique barre la route de l’Ouest et oblige l’Espagne à la contourner. Un Portugais se met alors à son tour au service de l’Espagne : à la tête de cinq navires, Fernand de Magellan entreprend en 1519 ce qui devient la première circumnavigation terrestre. Ce voyage prouve la sphéricité de la Terre et aboutit à une estimation de sa circonférence proche de celle d’Ératosthène.
L’époque moderne (1633–1900)
La circonférence polaire de la Terre est précisée en 1670 par l’abbé Picard qui, en réalisant des mesures de méridien entre la Picardie et l’Essonne, l’évalue à 20 541 600 toises, soit 40 036 km.
Le saviez-vous ?
Contrairement à une confusion courante, Galilée n’a rien découvert de particulier sur la forme et les dimensions de la Terre. Les travaux qui l’ont opposé à l’inquisition portent sur l’héliocentrisme, qui n’était pas accepté au XVIIe siècle car il contredisait les affirmations d’Aristote. Galilée a été condamné à la prison à perpétuité mais le pape Urbain VIII a immédiatement commué sa peine en résidence à vie. Galilée est mort à 78 ans, chez lui près de Florence.
Mais un nouveau rebondissement secoue la forme et les dimensions de la Terre au XVIIIe siècle. En étudiant des mesures effectuées au sud de la France, Jacques Cassini (dit Cassini II, 1677–1756) déduit que la Terre n’est pas une sphère parfaite mais doit être allongée aux pôles à la manière d’un ballon de rugby. Mais cette conclusion contredit certaines autres observations, notamment sur les oscillations du pendule aux différentes latitudes, qui tendent à prouver le contraire. Une controverse de quinze ans oppose Cassini aux partisans d’Isaac Newton (1643–1727), qui défendent l’idée d’une Terre aplatie.
Pour trancher la question, la France envoie deux expéditions, en Laponie et au Pérou, dans le but de mesurer très précisément les longueurs d’un degré de méridien dans des conditions de latitude extrêmes – leur comparaison devant confirmer l’une ou l’autre des théories. Mais la certitude sera acquise par Nicolas-Louis de la Caille (1713–1762) et le fils de Cassini II, César-François Cassini de Thury (dit Cassini III, 1714–1784), avant même les résultats des expéditions. En comparant des mesures réalisées en Provence avec celles du méridien de Paris, ils valident l’hypothèse de Newton en 1744.
Lorsqu’éclate la Révolution Française, on sait que la Terre est un sphéroïde de révolution aplati aux pôles, c’est-à-dire un ellipsoïde dont l’aplatissement est évalué par Pierre-Simon Laplace (1749–1827) entre 1/250 et 1/320ème. Avec l’avènement des idéaux des Lumières émergent des aspirations universelles, car rien n’a vraiment changé depuis l’Antiquité : chaque pays, voire chaque région, a ses propres unités de mesure auxquelles il est nécessaire de s’adapter à chaque passage de frontière. La France décide d’établir un nouveau système, qu’elle veut universel, appuyé sur une longueur commune au monde entier : la circonférence polaire de la Terre.
Dès 1792, le Marquis de Condorcet (1743–1794) demande aux astronomes Jean-Baptiste Delambre et Pierre Méchain de mesurer aussi précisément que possible le méridien de Paris entre Dunkerque et Barcelone. Grâce à leurs travaux, une nouvelle unité de mesure est créée en 1795 : le mètre est défini comme le quart du dix millionième du méridien terrestre. Il faut toutefois noter que cette unité "universelle" reste très française : en réalisant la triangulation de l’Inde, William Lambton (1753–1823) effectue une mesure de méridien qui, si elle avait servi d’étalon, aurait abouti à une unité de mesure légèrement plus courte.
Dès le XIXe siècle, les géodésiens étudient l’épineux problème de la gravité, dont l’importance sur la forme de la Terre avait été démontrée dès 1743 par Alexis-Claude Clairaut. Charles Lallemand (1857–1938) est le premier à en tenir compte pour réaliser le nivellement général de la France qui porte son nom. Toutefois, la difficulté de mesurer la pesanteur terrestre réelle le conduit à se contenter de la décrire par un modèle mathématique global.
Forme de la Terre et gravimétrie
Comme précisé en début d’article, la forme de la Terre désigne une surface parfaitement horizontale. Mais l’horizontale n’est que la perpendiculaire à la verticale, qui est définie comme la direction du fil à plomb. Selon la loi de la gravité, les corps massifs attirent les plus légers. Sur Terre, le fil à plomb est donc avant tout attiré vers le centre de l’énorme masse qu’est la planète elle-même. Mais la Terre n’est pas de composition interne homogène : il existe dans sa croûte et son manteau des masses plus denses que leur environnement immédiat. Elles-mêmes exercent une force de gravitation qui leur est propre et attirent le fil à plomb, déviant dès lors sa direction première. Or si la verticale est déviée, sa perpendiculaire horizontale l’est aussi, ce qui affecte par conséquent la forme de la Terre.
Le XXe siècle
En 1912, une nouvelle théorie relègue la question de la pesanteur au second plan. Dans La Genèse des continents et des océans, le climatologue allemand Alfred Wegener (1880–1930) suppose qu’en des temps très reculés, il n’existait qu’une seule masse continentale qui se serait fractionnée pour donner naissance aux continents actuels ; lesquels, d’après lui, continuent à dériver à la surface du globe ; toujours d’après lui, ce mouvement expliquerait la formation des chaînes de montagnes et les tremblements de terre.
Pour appuyer sa théorie, il convoque nombre d’observations multidisciplinaires : géographie (la complémentarité des côtes africaine et sud-américaine), paléontologie (les similitudes de fossiles en des endroits éloignés), climatologie (les traces de changements climatiques inexplicables de manière globale), entre autres.
S’appuyant sur la théorie orthodoxe selon laquelle le relief s’explique par le refroidissement de la Terre, bien des scientifiques tournent les idées de Wegener en ridicule en lui demandant de désigner la force phénoménale qui pourrait générer un mouvement de masses telles que les continents. Or Wegener ne peut proposer aucune explication satisfaisante à ce sujet. Cette force n’est affirmée qu’en 1931 par le géologue anglais Arthur Holmes (1890–1965), quelques mois après la mort de Wegener au Groenland : les mouvements de convection du manteau terrestre.
Les progrès techniques de l’après-guerre relancent ensuite les questions sur le champ de gravité terrestre, laissées en semi-suspens depuis plus de cinquante ans. La trajectoire de Spoutnik, le premier satellite artificiel lancé en 1957 par l’Union Soviétique, donne aux géodésiens une première idée des déformations générales de l’ellipsoïde terrestre.
Les satellites suivants enrichissent et précisent les mesures, jusqu’au lancement de la première constellation de positionnement spatial américaine : TRANSIT. Ses données ouvrent la voie à la modélisation de la forme réelle de la Terre : le géoïde. Déformé comme une patate par les déviations de la verticale dues à l’hétérogénéité des masses internes de la planète, il accuse des écarts géométriques d’environ 200 m d’amplitude par rapport à l’ellipsoïde parfait.
Toutefois, comme il est impossible de tracer un système de coordonnées sur un volume irrégulier, les géographes ont choisi d’assimiler la planète à un véritable ellipsoïde afin de transcrire les informations de longitude et de latitude. Calculé en 1980, l’ellipsoïde IAG-GRS80 moyenne au mieux les déformations du géoïde. Utilisé dès le départ comme la référence terrestre du système GPS, il est aujourd’hui intégré dans le référentiel géodésique international ITRS.
Épilogue
Les connaissances acquises à la fin du siècle dernier autorisent à affirmer que la forme et les dimensions de la Terre ont enfin livré tous leurs secrets. Mais les déformations du globe promettent aux géodésiens d’être encore loin, très loin du bout de leurs peines en matière de système de coordonnées mondial : les utilisateurs des systèmes GNSS (positionnement par satellites) ne cessent de demander une précision toujours plus drastique pour des applications de plus en plus exigeantes. L’ordre de grandeur de la précision actuellement recherchée est le millimètre. Mais se positionner au millimètre près sur une patate en perpétuelle déformation aléatoire n’est pas une tâche facile...
Bibliographie
- Le Timée par Platon, éditions Flammarion (2017) - ISBN 2-081421-56-9
- Pour l'histoire de la science hellène par Paul Tannery, Revue Philosophique de Louvain (1932) (disponible sur Wikisource)
- La Genèse des continents et des océans par Alfred Wegener, éditions Bourgeois (1991) - ISBN 2-267008-01-7
- Histoire de la cartographie par Georges Alhinac (1986)
- Mesurer la Terre par Jean-Jacques Levallois, éditions AFT (1988) – ISBN 2-907586-00-9
- Les Sciences géographiques dans l’Antiquité par Raymond D’Hollander, éditions AFT (2002) – ISBN 2-901264-53-0
- La grande aventure de la cartographie par Beau Riffenburgh, éditions National Geographic (2011) – ISBN 2-845823-66-5
- Histoire universelle de la navigation – tome 1 : les découvreurs d’étoiles par François Bellec, éditions De Monza (2016) – ISBN 2-916231-44-7
Webographie
